Introduction
The last lecture introduced the course. This lecture re-introduces you to some of the concepts you learned last year in Dr. Lenihan's class. The concept of utility has a long and convoluted history in economics, and has been discussed since at least 1748. The idea of choice theory is to make a statement about what choices a rational person should make, based on their preferences, among competing alternatives. It will turn out that people's desires are infinite, while their budgets are often much more limited. The constraints individuals work under, combined with their prestated preferences, turn out to be the important factors in creating the theory of choice. First, let's talk about utility.
Important Concepts. Budget constraint, utility function, indifference curve, marginal utility, marginal rate of substitution.
Definition. Utility is the satisfaction a person receives from their economic activities.
To get a measure of utility, we will need to make some assumptions about the world.
- Ceteris Paribus. Holding other factors constant, we can think about measuring utility because other choices outside the ones we are considering are not affected by the choices we make now.
- Utility Function. There need to be at least 2 goods in a model of economic choice. Most of the time there are many more. The mechanism we use to describe how the consumer combines their utility is called the utility function. For each combination of goods, call them
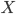and 
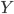, the function pumps out a level of utility, 
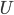, holding everything else constant.
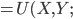everything else) Assumptions about Preferences
- Transitivity. If there are three goods,
, 
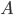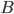, and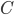 
, then our consumer can choose between them. If he prefers 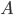to 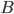, and prefers 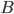to 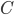, then he must prefer 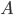to 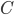. - Completeness. For any list of goods we give him, our consumer has to be able to make a choice between those goods, and rank them, because the assumption of transitivity must hold.
- More Preferred to Less. If the good is normal, so if your income increases, you'll demand more of it, you will always prefer more stuff to less stuff.
Indifference Curves
These are tricky little beasts, so it is wise to spend some time working on drawing them.
Think of an indifference curve like a contour map of a mountain. The indifference curve represents a set of points (called a locus) where, for each consumer, each point represents a combination of goods which makes them equally happy. The consumer will always want to be higher up the mountain of happiness, so to speak, but if they have to stay there, then they will be indifferent between the alternatives on that line. Click the image below to get an excel file to manipulate. In class we'll use a mathematica demonstration.
Diminishing Marginal Rate of Substitution. The MRS is the slope of the indifference curve, and it encapsulates the idea that you will be willing to give up a certain number of units of
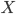to get more units of 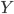on the same indifference curve. The MRS is the ratio between the marginal utilities (
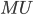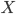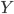) of each good, and , so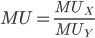 
The MRS stops moving along the indifference curve when ratio between the prices of each good,
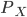and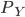 
is equal to the value of the MRS. We'll have something like
.
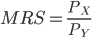Because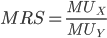 
, it follows that
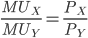
All this says is that the ratio of the extra utility for consuming one more unit of either good to its price should be the same for each good. Now, where do we get the prices from? We get them from the budget constraint.
Budget Constraint. The budget constraint shows the combinations of the two goods the consumer can afford, given that they have a fixed amount of income. The budget curve is downward-sloping because to get more of good 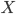, you're going to have to give up some of good .
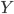The budget constraint looks like this:
We'll put the two diagrams together in class using the mathematica demonstration.
Exercises to test your understanding in the book: Ex. 2.1, 2.2, 2.9.
In the next lecture, we'll look at individual demand curves.
lectures r great, at least i'm not falling asleep. explanations r in good English so easy to understand. suggestion: please bring fruit next time for ur experiment instead of Crunchy, coz it would be much healthier! Your r doing a great job, very good approach to presenting lectures, very enjoyable!!!!!