In the last few lectures, we've looked at growth theory and the stakes involved in getting the basics wrong. We saw the Solow model's predictions about sustained capital accumulation (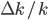 ): keep population growth low, keep savings (
): keep population growth low, keep savings (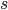 ) and therefore investment(
) and therefore investment(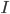 ) rather high, and try to curb depreciation on assets. Technical progress and human capital move the economy forward, potentially stimulating convergence of growth rates.
) rather high, and try to curb depreciation on assets. Technical progress and human capital move the economy forward, potentially stimulating convergence of growth rates.
Now we'll move onto a micro-founded macro model developed in the later chapters of the Barro book. The basic idea is to specify four markets inside the economy: the products market, the bond market, the money market, and the labour market. We'll build our macroeconomic equilibria from behavioural assumptions about the actors in the model: households and firms. Households are assumed to want to maximise their incomes from all of these markets, subject to a budget constraint. Firms want to maximise profits. Their interactions, along with the usual macroeconomic accounting identities, such as 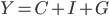 , give us the macroeconomic equilibrium, called a general equilibrium.
, give us the macroeconomic equilibrium, called a general equilibrium.
Click the link below to download slides, handouts, etc.
Click the link below to download papers and interviews about growth, technical progress, and the micro-founded macro model.
