[print_link]
The theory of production of commodities by means of commodities has a long history in economics. From the earliest recorded thinking about how households manage their inputs and outputs through to the modern day, the concern with how and why and what people produce in order to satisfy their needs and desires has been at the core of economics.
So it's important you have a look at the main approach to thinking about production.
We have a function, which is a rule which specifies, for each value of 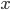 , in the domain of
, in the domain of 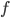 , prescribes a unique value of
, prescribes a unique value of 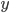 such that
such that 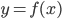 . We always want a function to be able to answer the question: 'Given a numerical value of
. We always want a function to be able to answer the question: 'Given a numerical value of 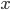 , what is the unique corresponding numerical value
, what is the unique corresponding numerical value 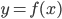 '?
'?
The core idea of today's lecture is that the firm is just a machine which produces outputs from given inputs. Workers work the machines and receive a wage, and capitalists own the machines, and received profits (or losses) for their investment in the machines.
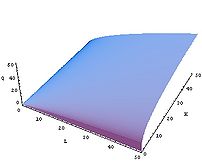
We represent the relationship between a firm's inputs and its outputs through a production function, which specifies how many units of output you'll get for a given combination of inputs.
What kinds of inputs are we talking about here? We have to consider hours of labour,  , spent on the production of the good, the amount of capital
, spent on the production of the good, the amount of capital 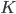 spent in getting the productive capacity ready to actually crank out units of the good, and amounts of raw materials
spent in getting the productive capacity ready to actually crank out units of the good, and amounts of raw materials 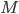 used up in the productive process. We summarise the relationship between inputs and outputs through the production function, which takes the form
used up in the productive process. We summarise the relationship between inputs and outputs through the production function, which takes the form
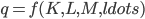 .
.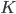 , and labour,
, and labour,  , are used in the production of the good, so our production function becomes
, are used in the production of the good, so our production function becomes
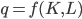 .
.The marginal product of a production process asks the same type of question as marginal utility. The basic idea is to ask how much extra output of 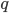 one might get for a one unit increase in the level of capital or labour used as inputs.
one might get for a one unit increase in the level of capital or labour used as inputs.
We have two definitions then: marginal product of labour, and marginal product of capital. It's worth writing these down somewhere, and checking the textbook for examples.
Marginal product of labor (MPL): the extra output obtained by employing one more unit of labor while holding the level of capital equipment constant.
Marginal product of capital (MPK): the extra output obtained by using one more machine while holding the number of workers constant.
We'll look at the relationship between total product, marginal and average product, and levels of output, using this Mathematica demonstration.
Isoquants
Once you have calculated the optimal level of output consistent with marginal products of labour and capital, one can think about trying to get the most output from differing combinations of those inputs. We'll study Leontieff-type production functions using this Mathematica demonstration.
We use the isoquant to show us outputs of the same level produced with different combinations of labour and capital. The isoquant map is infinite, meaning for any combination of capital and labour, one can find an isoquant at that combination. The isoquant is similar to the indifference curve we saw in earlier lectures, because each represents the contour of a surface, or the 'altitude' of production. The slope of the isoquant is given by the change in capital input divided by the change in labour input, a relationship we'll call the rate of technical substitution.
The Marginal Rate ot Technical Substitution (RTS) is the amount by which one input can be reduced when one more unit of another input is added while holding output constant (i.e. negative of the slope of an isoquant).
Mathematically we can solve for the RTS by calculating
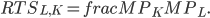
Returns to Scale
A production function is said to exhibit constant returns to scale if a doubling of all inputs results in a precise doubling of output. If doubling all inputs results in more than a doubling of output, the production function exhibits increasing returns to scale. Although an intellectual storm has raged about the assumptions underlying returns to scale, in practice most mainstream economists assume CRTS for simplicity. Whether this is a good idea is the subject of a more advanced course.
Changes in Technology
Technology affects the production of goods, so we add another element to the production function to take account of the changes in technology. Call this element 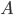 , and our production function becomes
, and our production function becomes
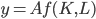 .
.This function says technology affects capital and labour in the same way. We measure the components of 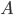 using total factor productivity.
using total factor productivity.
Exercises to try:
7.2, 7.3, 7,7.
Next lecture: Costs, read chapter 8.
Related articles
- The political economy of networks
- Complements in production
- Is factor productivity due to revert to its long-run mean?
- Where's the production function?