In the last lecture we looked at the theory of choice. Today its all about demand. Click below for lecture notes, which you can print using the print icon below.
[print_link]
Introduction
The theory of demand concerns behavioural adaptation and change in response to different circumstances. The idea is that a demand curve represents a cloud of 'what ifs', where different prices are called out and the consumer then decides how many units of a good to buy or consume.
The demand function is a correspondence between the quantity of some good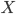 
demanded, and the price of 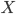, the existence of alternatives like 
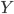, and the individuals income, 
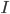. Finally, using the ceteris paribus assumption we discussed last week, we hold all the other factors which might have some effect on demand (like time, place, elevation, and so forth) constant. The demand function is given by
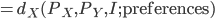
Preferences are included after the semi colon because we want to show that most of the time, preferences don't change.
Caution. Be careful when discussing changes in the demand curve. The only thing which causes a movement in quantity demanded is a change in the good's price. If anything else (like preferences or the price of another good) changes then that is a shift in demand.
The demand function has a few properties we need to talk about.
Homogeneity
This is a simple idea with a complicated title. If you double the prices and the income available for the purchase of 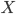and 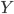, then quantity demanded won't change. If we assume a budget constraint like
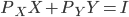
which is the same as
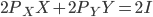
Substitution and Income Effects
Definition. The Substitution Effect is the effect due only to the relative price change, controlling for the change in real income.
In order to compute it we ask: what is the bundle that would make the consumer just as happy as before the price change, but if they had to make their choice faced with the new prices. To find this point we consider a budget line characterized by the new prices but with a level of income such that it is tangent to the initial indifference curve.
Definition. The Income Effect is the effect due to the change in real income.
For example, when the price goes up the consumer is not able to buy as many bundles that she could purchase before. This means that in real terms she has become worse off. The effect is measured as the difference between the “intermediate" consumption” and the final consumption which I'll show in class.
Unlike the Substitution Effect, the Income Effect can be both positive and negative depending on whether the product is a normal or inferior good. By construction, the Substitution Effect plus the Income Effect equals the total effect of the price change.
We'll use a mathematica demonstration to show the substitution and income effects in class.
Application
Let's give first time house buyers their income tax back if they want to buy houses this year and next.
Consumer Surplus
Consumer surplus is all about measurement. We want to measure the changes under the demand curve from a change in price. Geometrically, we can measure changes in the area under the demand curve, and because the demand curve measures utility in some sense, then we can say utility has increased or decreased. It's a cool idea, and we'll spend a few minutes on it.
We'll use a mathematica demonstration to show the changes in consumer surplus.
Examples to try: 3.4, 3.5, 3.1
Important Concepts: Demand Curve, Demand Function, Income Effect, Substitution Effect.